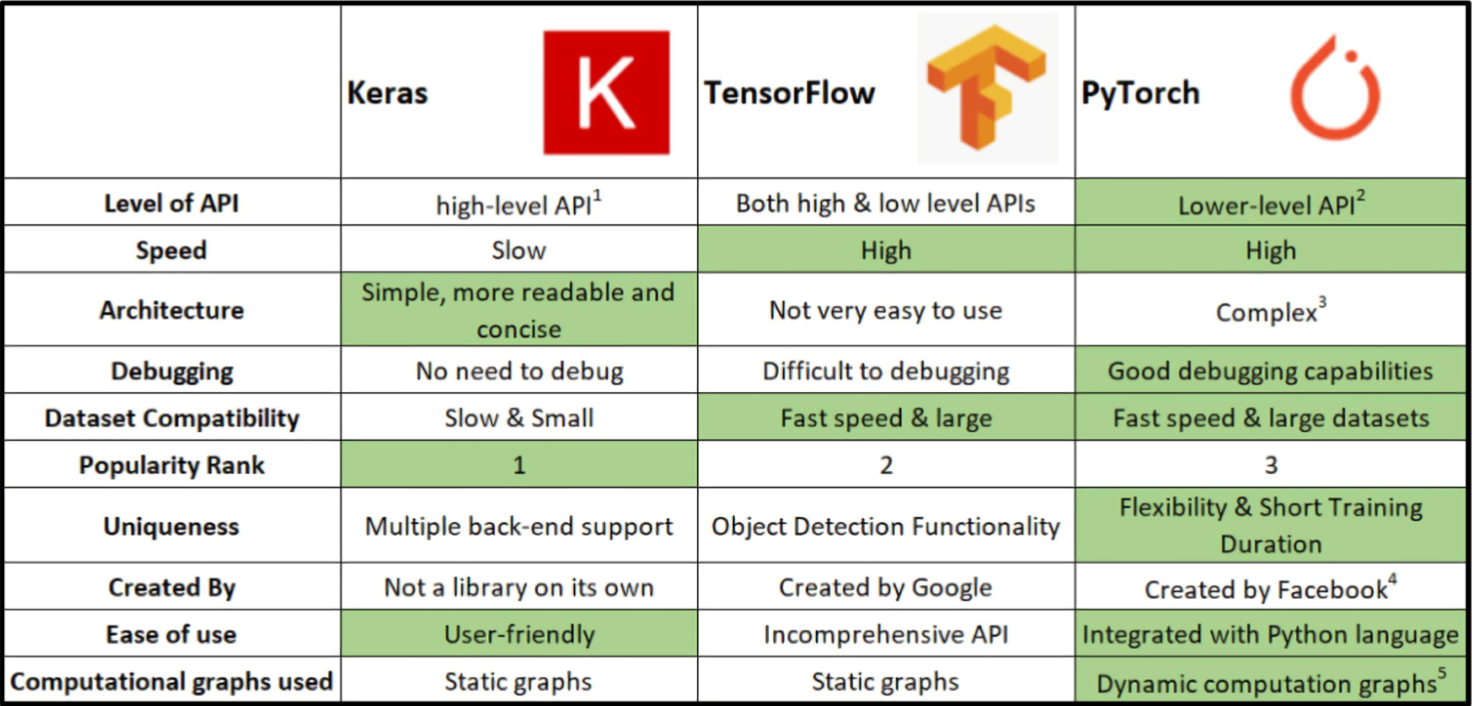
PyTorch = Numpy + AutoGrad

라는 개인적인 공식에 맞게 Numpy에 대해 알면 PyTorch 를 이해하기 쉽다. 

가장 중요한 AutoGrad와 함께 PyTorch Operations 에 대해 알아보자

1. Tensor

• 다차원 Arrays 를 표현하는 PyTorch 클래스
• Numpy의 ndarray와 동일, TensorFlow의 Tensor와도 동일
• Tensor를 생성하는 함수도 거의 동일

# Numpy - ndarray
import numpy as np
n_array = np.arange(10).reshape(2,5)
print(n_array)
print("ndim :", n_array.ndim, "shape :", n_array.shape)

# PyTorch - tensor
import torch
t_array = torch.FloatTensor(n_array)
print(t_array)
print("ndim :", t_array.ndim, "shape :", t_array.shape)

[[0 1 2 3 4]
 [5 6 7 8 9]]
ndim : 2 shape : (2, 5)
tensor([[0., 1., 2., 3., 4.],
              [5., 6., 7., 8., 9.]])
ndim : 2 shape : torch.Size([2, 5])

1-1. numpy like operations

기본적으로 PyTorch의 대부분의 사용법이 그대로 적용됨

data = [[3, 5, 20],[10, 5, 50],[1, 5, 10]]
x_data = torch.tensor(data)

x_data[1:]
# tensor([[10, 5, 50],
#        [ 1, 5, 10]])
          
x_data[:2, 1:]
# tensor([5, 20],
#        [5, 50]])
         
x_data.flatten()
# tensor([3, 5, 20, 10, 5, 50, 1, 5, 10])

torch.ones_like(x_data)
# tensor([[1, 1, 1],
#         [1, 1, 1],
#         [1, 1, 1]])
          
x_data.numpy()
# array([[ 3, 5, 20],
#        [10, 5, 50],
#        [ 1, 5, 10]], dtype=int64)

x_data.shape
# torch.Size([3,3])

x_data.dtype
# torch.int64

1-2. Numpy Vs PyTorch

• PyTorch의 tensor는 GPU에 올려서 사용가능

data = [[3, 5, 20],[10, 5, 50],[1, 5, 10]]
x_data = torch.tensor(data)

x_data.device
# device(type='cpu')

# GPU를 사용할 수 있는지 확인 (M1 MAC 환경)
device = torch.device("mps") if torch.backends.mps.is_available() else "cpu"
print(f"device: {device}")

# GPU 상에서 실행 (M1 MAC 환경)
x_data = torch.tensor(data, device=device)
print(x_data)

cpu
device: mps
tensor([[ 3,  5, 20],
        [10,  5, 50],
        [ 1,  5, 10]], device='mps:0')  <- mps:0이 출력되어야 GPU 사용한 것

2. Tensor handling

• view, squeeze, unsqueeze 등으로 tensor 조정가능
• view : reshape과 동일하게 tensor의 shape을 변환
• squeeze : 차원의 개수가 1인 차원을 삭제 (압축)
• unsqueeze : 차원의 개수가 1인 차원을 추가

2-1. view

tensor_ex = torch.rand(size=(2, 3, 2))
print(tensor_ex)
# tensor([[[0.6388, 0.0342],
#          [0.2073, 0.5346],
#          [0.3281, 0.5916]],

#        [[0.5568, 0.2371],
#         [0.0448, 0.7719],
#         [0.0505, 0.3120]]])

print(tensor_ex.view([-1, 6]))
# tensor([[0.6195, 0.0416, 0.6620, 0.1878, 0.8998, 0.7728],
#        [0.1560, 0.6493, 0.2845, 0.1738, 0.0421, 0.9934]])

print(tensor_ex.reshape([-1, 6]))
# tensor([[0.6195, 0.0416, 0.6620, 0.1878, 0.8998, 0.7728],
#        [0.1560, 0.6493, 0.2845, 0.1738, 0.0421, 0.9934]])

2-2. squeeze & unsqueeze

tensor_ex = torch.rand(size=(2, 1, 2))
tensor_ex.squeeze()
# tensor([[0.8510, 0.8263],
#         [0.7602, 0.1309]])

tensor_ex = torch.rand(size=(2,2))
tensor_ex.unsqueeze(0).shape
# torch.Size([1, 2, 2])
tensor_ex.unsqueeze(1).shape
# torch.Size([2, 1, 2])
tensor_ex.unsqueeze(2).shape
# torch.Size([2, 2, 1])

3. Tensor Operation

• 행렬곱셈 연산은 dot이 아닌 mm 사용, 벡터내적은 dot 가능
• matmul 은 broadcasting을 지원해준다. -> 헷갈릴 수 있음.  -> mm 사용

n2 = np.arange(10).reshape(5,2)
t2 = torch.FloatTensor(n2)

t1.mm(t2)
# tensor([[ 60.,  70.],
#         [160., 195.]])

t1.dot(t2)
# RuntimeError

t1.matmul(t2)
# tensor([[ 60.,  70.],
#         [160., 195.]])

4. nn.functional Module

• nn.functional 모듈을 통해 softmax, one_hot, cartesian_prod 등 많은 기능 제공

# softmax 와 one_hot 예
import torch
import torch.nn.functional as F

tensor = torch.FloatTensor([0.5, 0.7, 0.1])
h_tensor = F.softmax(tensor, dim=0)  # dim 은 axis 와 같다.
h_tensor
# tensor([0.3468, 0.4224, 0.2318])

y = torch.randint(5, (10,5))
y_label = y.argmax(dim=1) 

print(torch.nn.funtional.one_hot(y_label))  # one_hot 적용

tensor([[0, 1, 0, 0, 0],
        [0, 1, 0, 0, 0],
        [1, 0, 0, 0, 0],
        [1, 0, 0, 0, 0],
        [1, 0, 0, 0, 0],
        [0, 0, 1, 0, 0],
        [0, 0, 0, 0, 1],
        [1, 0, 0, 0, 0],
        [1, 0, 0, 0, 0],
        [1, 0, 0, 0, 0]])

# cartesian_prod 예
import itertools
a = [1, 2, 3]
b = [4, 5]
list(itertools.product(a, b)) # 모든 경우의 수를 구해줌

tensor_a = torch.tensor(a)
tensor_b = torch.tensor(b)
print(torch.cartesian_prod(tensor_a, tensor_b)) # 모든 경우의 수를 구해줌

tensor([[1, 4],
        [1, 5],
        [2, 4],
        [2, 5],
        [3, 4],
        [3, 5]])

5. AutoGrad

• PyTorch의 핵심은 자동 미분의 지원 -> backward 함수 사용
• 미분의 대상이 되는 것을 requires_grad=Ture 로 한다. (대부분 weight 값)

# Ex1
w = torch.tensor(2.0, requires_grad=True)  # w = 2 이고, w에 대해 미분가능
y = w**2
z = 10*y + 25
z.backward()  # .backward() 가 미분 명령어
print(w.grad)

tensor(40.)

# Ex2
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
Q = 3*a**3 - b**2
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)

print(a.grad)
print(b.grad)

tensor([36., 81.])
tensor([-12.,  -8.])

PyTorch, TensorFlow 등 프레임워크의 도움으로 더 이상 밑바닥부터 딥러닝을 구현하지 않아도 된다.

현재는 반복적인 작업을 누군가 미리 만들어 놓은 프레임워크를 사용하기 때문이다.

그럼, 프레임워크가 무엇인지. 딥러닝 프레임워크들에는 무엇이 있는지 더 알아보자.

1. 프레임워크란?

 프로그램을 다룸에 있어 공통적으로 사용되는 기능들을 표준화된 소스코드로 만들어 놓고 사용할 수 있도록 제공하는 것

2. 딥러닝 프레임워크의 종류와 특징 

• 대표적으로 Google에서 개발된 TensorFlow 와 Meta(구 Facebook)에서 개발된 PyTorch 가 있다.
• 두 프레임워크의 가장 큰 차이점은 Define and Run 과 Define by Run 에 있다.
• Keras는 TensorFlow 2.0이 나오면서 TensorFlow와 합쳐졌다.

3. Define and Run vs Define by Run

Computational Graph(연산의 과정을 그래프로 표현한 것)를 언제 생성하느냐에 따라 구분한 것

• Define and Run : 그래프를 먼저 정의 -> 실행시점에 데이터 feed
• Define by Run : 실행을 하면서 그래프를 생성하는 방식(Dynamic Computational Graph, DCG)

4. Why PyTorch ?

• Define by Run 의 장점 -> 즉시 확인 가능 -> pythonic code
• GPU support (Multi-GPU)
• 자동미분을 지원하여 DL 연산을 지원

DL 프레임워크로 PyTorch가 적절한 것 같아

앞으로 PyTorch를 좀 더 공부해볼 계획이다.